Las leyes de Kirchhoff son dos igualdades que se basan en la conservación de la energía y la carga en los circuitos eléctricos. Fueron descritas por primera vez en 1845 por Gustav Kirchhoff.
Ambas leyes de circuitos pueden derivarse directamente de las ecuaciones de Maxwell, pero Kirchhoff precedió a Maxwell y gracias a Georg Ohm su trabajo fue generalizado. Estas leyes son muy utilizadas en ingeniería eléctrica para hallar corrientes y tensiones en cualquier punto de un circuito eléctrico.
Esta ley es llamada también Segunda ley de Kirchhoff, ley de lazos de Kirchhoff y es común que se use la sigla LVK para referirse a esta ley.
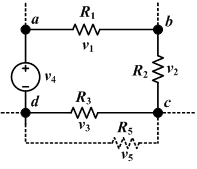
Ley de tensiones de Kirchhoff, en este caso v4= v1+v2+v3. No se tiene en cuenta a v5 porque no hace parte de la malla que estamos analizando.
En toda malla la suma de todas las caídas de tensión es igual a la tensión total suministrada. De forma equivalente, En toda malla la suma algebraica de las diferencias de potencial eléctrico es igual a 0.
Ambas leyes de circuitos pueden derivarse directamente de las ecuaciones de Maxwell, pero Kirchhoff precedió a Maxwell y gracias a Georg Ohm su trabajo fue generalizado. Estas leyes son muy utilizadas en ingeniería eléctrica para hallar corrientes y tensiones en cualquier punto de un circuito eléctrico.
Esta ley es llamada también Segunda ley de Kirchhoff, ley de lazos de Kirchhoff y es común que se use la sigla LVK para referirse a esta ley.
Ley de tensiones de Kirchhoff, en este caso v4= v1+v2+v3. No se tiene en cuenta a v5 porque no hace parte de la malla que estamos analizando.
En toda malla la suma de todas las caídas de tensión es igual a la tensión total suministrada. De forma equivalente, En toda malla la suma algebraica de las diferencias de potencial eléctrico es igual a 0.